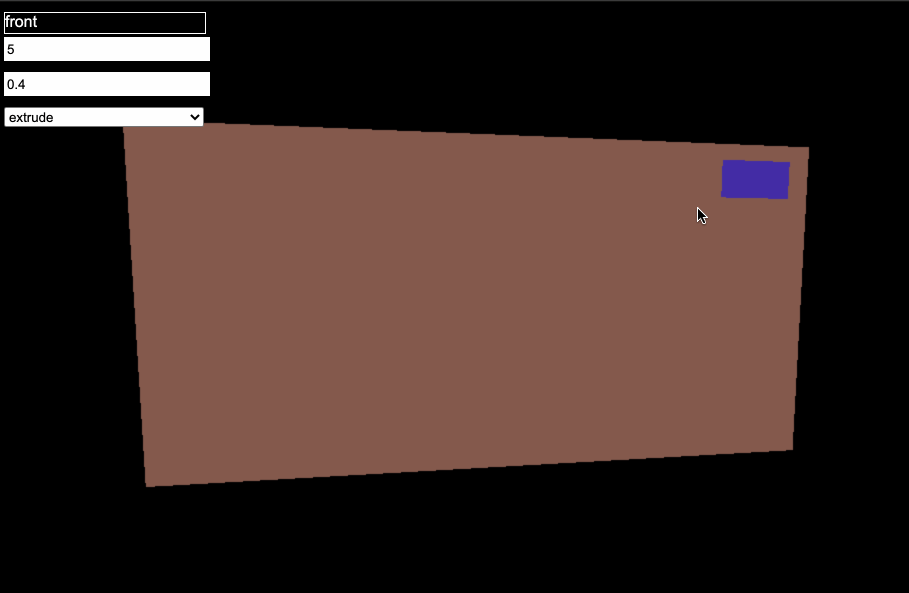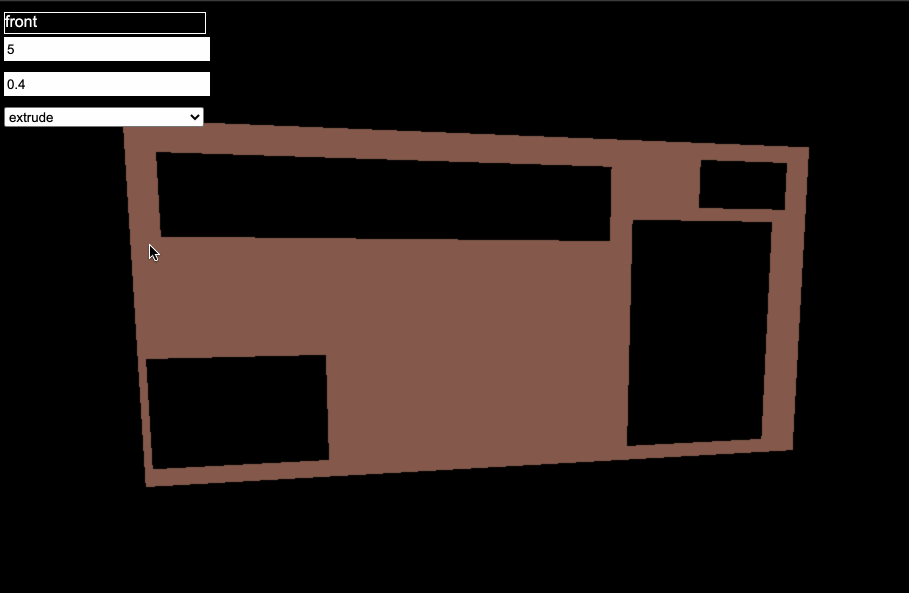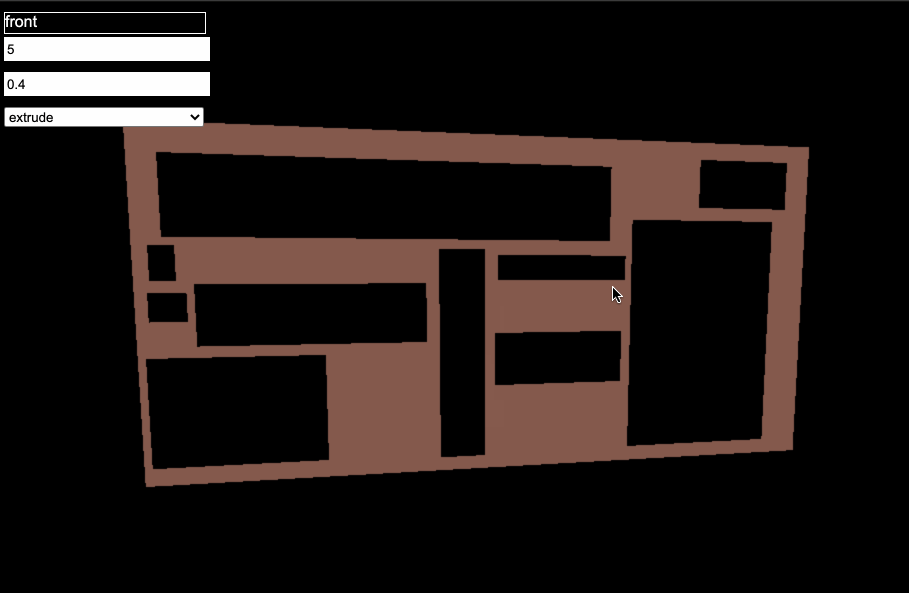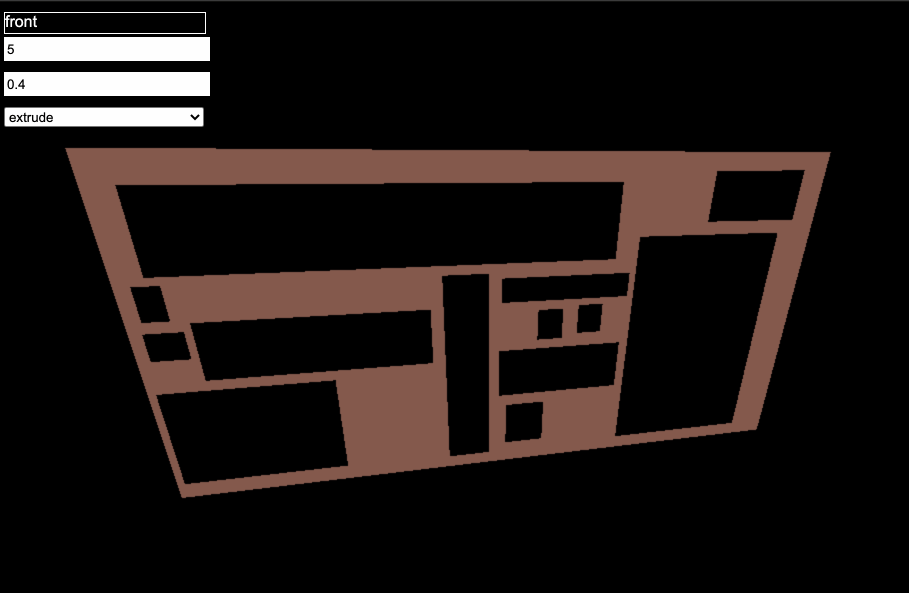
I’m continuing to work on my web-based parametric modeler for 3d-printable tech panels, and I finally solved what will likely be the hardest problem in the whole (pun not intended) project- supporting multiple holes.
At the start, the system creates six quads that can each receive mouse events. When the user holds space and click-drags to specify a new feature’s location, a couple of things happen, namely:
- A new hole is added to the existing quad
- The existing quad re-generates its faces to fill in everywhere except the hole (or holes)
- The new feature is created, with the hole’s points as its basis
The second step above was the doozy. If there’s only a single hole in a quad, it’s very easy to fill in the necessary faces. This is especially true since I’m making sure that quads are always represented with their points in clockwise order starting at the top left.
However, if there are multiple holes, it gets tricky. One solution would be to throw all the points into a collection and create a Deluany triangulation, but I thought I could leverage the constraints built into my system to my advantage and do something a bit simpler.
Ultimately I ended up writing my own algorithm that sweeps across from left to right, adding the vertical edges of the holes one at a time and creating triangles as needed.
The approach is to:
- create two vertical edges for each hole
- sort all of the edges by X-coord
- init a sweep line with the bottom-left and top-left points of the parent quad
- for each edge starting with the left-most:
- start with the bottom vert
- find either the two or three (see below) vertices in the sweep line that are directly above and below the new vert, and connect them to the vert that’s currently being inserted
- insert the new vert into the sweep line at the appropriate position
- after each edge is inserted, run along the vertices of the sweep line and check for any concavities. If any three vertices form a concave curve, connect the first and last with a triangle to make it convex
- once all of that is done, finish off the quad by connecting the top-right and bottom-right vertices of the original quad to the remaining vertices of the sweep line
You might have noticed that nothing about the above mentioned removing vertices from the sweep line. You may have also noticed that I mentioned that we get either two or three vertices when comparing a new vertex to the sweep line. One of those provides the answer to the other.
Since everything, both the parent and the holes, are quads, that means that sometimes we’ll have a new vertex that has exactly the same Y-coord as an existing vertex in the sweep line (since we’re inserting the right-hand edge of a hole that already had its left-hand edge inserted). In that case, we get three vertices:
- the vertex in the sweep line that’s below the new vert
- the vertex in the sweep line that’s equal to the new vert (in Y-pos)
- the vertex in the sweep line that’s above the new vert
In such a case, the algorithm connects the new vert to the middle and either the top or the bottom, whichever one *doesn’t result in the three vertices belonging to the same hole (since that would create a face inside the hole). It then removes the middle vert from the sweep line.
 Follow
Follow